Hydraulik
In diesem Kapitel möchten wir das Prinzip des Auftriebs verstehen.
Bevor wir uns jedoch an Auftrieb heranwagen können, müssen wir klären, was wir unter Dichte und Druck in der Physik verstehen.
Was ist Dichte ?
Gleich schwere Objekte können unterschiedlich groß sein.
Ein Kilogramm gasförmige Luft nimmt sehr viel Raum ein (830 Liter), wohingegen ein 1 Kilogramm flüssiges Wasser schon deutlich weniger Raum einnimmt (1 Liter).
Gewicht und Volumen hängen also offensichtlich zusammen. Diese Abhängigkeit wird in einer neuen physikalische Größe ausgedrückt der Dichte.
Die Dichte eines beliebigen \( \rho \) ist definiert als:
$$ \rho = \frac{m}{V} $$
die Größe m ist das Gewicht des Körpers und V ist das Volumen, das dieser Körper einnimmt.
In Worte gefasst fragt die Dichte danach, wie viel Gewicht pro eingenommenen Raum ein Körper hat.
Es ist also eine physikalische Größe, die Masse auf Volumen normiert.
In der Physik gibt es viele Dichten. Genau genommen wird der Begriff Dichte in der Physik wie eine Art Suffix verwendet.
Wenn wir in diesem Kapitel von Dichte reden, dann meinen wir damit immer die Massedichte.
Mit Massedichte meinen wir Masse pro Volumen.
Es gibt, wie bereits erwähnt, viele weitere Dichten, wie z.B. Ladungsdichte (Ladung pro Volumen) oder die Teilchendichte (Teilchen pro Volumen).
Der große Vorteil dieser physikalischen Einheit ist, dass wir mit ihr nun unterschiedlich große Objekte mit einander vergleichen können.
Überprüfe dein Wissen mit diesem Quiz:
Was ist Druck ?
Bei der Dichte wird gefragt, wie viel Masse auf ein bestimmtes Volumen kommt.
Wir können für Kraftwirkungen einen ähnlichen Begriff einführen, den sogenannten Druck.
Doch bevor wir zur Definition kommen, sollten wir uns fragen, warum die Definition dieser Größe sinnvoll ist.
Stellt euch vor, ihr steht inmitten von einem zugefrorenem See. Ihr wollt definitiv nicht, dass das unter euch Eis bricht. Die empfohlene Handlung bei diesem Unterfangen ist, nicht zu gehen, sondern zu robben. Beim Robben legt ihr euch auf den Bauch und schiebt euch zum besagtem Ziel, in unserem Fall zum Rand des Sees.

(Bild ist von der Wasserwacht Osterhofen übernommen – dort gibt´s viele Tipps, wie man sich richtig auf Eis verhält)
Doch warum sollte man das tun?
Ihr wiegt ja immer noch gleich viel, egal ob liegt oder steht. Die insgesamt auf das Eis übertragene Kraft ist also gleich groß.
Der Unterschied ist jedoch die Fläche, auf die die Kraft wirkt und sich verteilt.
Beim Robben verteilt ihr eure Kraft auf eine viel größere Fläche.
Dies führt dazu, dass ihr nicht die zum Brechen notwendige Kraft aufbringen könnt und das Eis hält.
Mit diesem kleinen Beispiel können wir nun auch klären was Druck ist:
Der Druck p ist eine Kraft F wirkend auf eine Fläche A:
$$ p = \frac{F}{A} $$
Merke dir:
Je größer die Fläche, bei gleicher Kraft, desto kleiner der Druck.
Der umgekehrte Fall gilt natürlich ebenso.
Die Physikalische Einheit des Druckes wird Pascal (Pa) genannt, ist jedoch nichts anderes als Newton pro Fläche.
Überprüfe dein Wissen mit diesem Quiz:
Herleitung des Schweredrucks:
Wir möchte nun herleiten woher z.B. der Luftdruck oder Wasserdruck in der tiefen See entsteht.
Dieser Druck wird Schweredruck oder hydrostatischer Druck genannt.
Wir werden im folgenden jedoch immer Schweredruck dazu sagen.
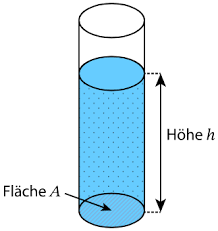
Im folgenden Bild seht ihr eine Wassersäule in einem Gefäß, in das ein Objekt eingetaucht worden ist.
Wir möchten nun den vom Wassergewicht erzeugte Druck qualitativ beschreiben.
Im Bild stellt A die Fläche der Wassersäule dar, h ist die Eintauchtiefe eines Objektes innerhalb des Gefäßes und g ist die Gravitationsbeschleunigung.
In dem Medium wird Kraft unter den Teilchen übertragen, durch pure elastische Stöße.
Die Wassermoleküle prallen also ineinander und verändern dabei nicht ihren internen Zustand.
Da die Teilchen jedoch unkontrolliert in alle Richtungen fliegen, spüren wir die Kraft nicht wirklich.
Jedes Wassermolekül wird zusätzlich noch durch die Gravitation der Erde in Richtung Erdmittelpunkt gezogen.
In unserem Teilchenbild drücken also alle Wassermoleküle zusätzlich noch von oben nach unten.
Da Wasser jedoch inkompressibel ist (also nicht komprimiert werden kann), verteilen sich diese Stöße auf die Fläche A und werden zu einem Druck.
Dieser Druck ist der besagte Schweredruck.
Auf diesen achten auch immer (Tiefsee-)Taucher*innen.
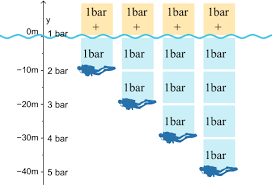
Wichtig hierbei ist, dass der Schweredruck wirklich nur von den Wassermolekülen über einem erzeugt wird.
Also der Druck hängt von der Eintauchtiefe h ab. Desto tiefer die Taucher*in eingetaucht ist, desto mehr Wasser befindet sich über ihr/ihm, und desto größer wird der Schweredruck.
Mit diesem Wissen können wir nun auch den Schweredruck mathematisch formulieren:
Dazu starten wir bei der Definition des Drucks: \( p = \frac{F_{G}}{A} \).
\(F_G\) ist die Kraft, die durch die Gravitation verursacht wird.
Diese Kraft ist nichts anderes als die Masse m multipliziert mit der Gravitationsbeschleunigung g der Erde:
$$ F_{G} = m \cdot g = \rho \cdot V \cdot g $$
Im letzten Teil der Gleichung nutzen wir aus, dass Dichte nichts anderes ist als Masse pro Volumen.
Alles eingesetzt führt zu:
$$ p = \frac{\rho V g }{A} $$
Das Volumen eines geraden Körpers, z.B. von unserem Gefäß, ist Fläche multipliziert mit der Höhe des Körpers: (\(V = A \cdot h\)).
Wenn wir diese Relation einsetzen, kürzt sich die Fläche aus unserer Gleichung.
Der Schweredruck lässt sich ausdrücken durch:
$$ p = \rho \cdot g \cdot h $$
Wir sehen in der Formel, dass der Schweredruck nur von der Dichte des Mediums und der Eintauchtiefe unseres Körpers abhängt.
Der treibende Faktor dieses Drucks ist die Gravitation. Der Schweredruck verändert sich also ebenfalls, wenn sich die Stärke der Gravitationskraft ändert.
Überprüfe dein Wissen mit diesem Quiz:
Schweredruck in der Atmosphäre:
Warum interessieren wir uns nun eigentlich für den Schweredruck? Der Grund ist, weil wir konstant von ihm umgeben sind.
Der Schweredruck existiert natürlich auch bei Gasen.
Der allgemeine Luftdruck in unserer Umgebung wird durch die Luftsäule über unseren Köpfen erzeugt.
Jedes Luftmolekül wird durch die Gravitation gegen uns gedrückt.
Mit der Formel für den Schweredruck können wir nun auch verstehen, warum der Luftdruck mit steigender Höhe abnimmt.
Zumal nimmt natürlich die Gravitationskonstante ab, zum anderen nimmt auch die über uns befindende Luftsäule ab.
Du kennst das vielleicht, wenn du schon mal im Gebirge unterwegs gewesen bist. Eventuell hattest du die ersten Tage richtig blöde Kopfschmerzen, da die Luft “dünner” ist und daher dein Körper Probleme hatte, genug Sauerstoff ins Blut zu bekommen.
Nach einiger Zeit produziert der Körper mehr Erythrozyten und kann dadurch mehr Sauerstoff aufnehmen. Wenn man wieder weiter unten unterwegs ist, dann ist man meist fitter.
Daher wird solch ein Höhentraining gerne von Spitzensportler*innen genutzt, um leistungsfähiger zu sein.
Schweredruck beim Blutmessen:
Zum Messen des Blutdruckes legt man eine aufblasbare Manschette um den Oberarm auf Herzhöhe an.
Die richtige Höhe ist entscheidend beim Messen des Blutdruckes, weil ansonsten der Schweredruck des Blutes das Messergebnis
verfälschen würde.
Je tiefer ihr messt, desto größer wird nämlich euer Blutdruck.
Im Fuß ist der Blutdruck also am höchsten, während er Kopf am niedrigsten ist.
Das kannst du dir schon mal für die Klinik merken 🙂
Und durch den Schweredruck haben auch viele Menschen geschwollene Füße und Beine. Daher hilft es, die Gliedmaßen hoch zu legen.
Schweredruck beim Wassertransport:
Warum fließt das Wasser aus dem Wasserhahn?
Natürlich weil der Druckunterschied innerhalb des Wasserhahnes größer ist zum Druck außerhalb des Hahnes.
Der Druck für den Wassertransport wird heutzutage mit Pumpen erzeugt, früher und auch noch in einigen hohen Gebäuden heute, werden Wassertürme verwendet. In Hamburg sind viele alte Wassertürme nun zu Wohn- oder Hotelgebäuden umgebaut worden, da die Pumpinfrastruktur alle versorgen kann.
Wassertürme sind hoch positionierte Türme, die mit einem dünnem Rohr mit der eigentlichen Wasserquelle verbunden sind.
Der Turm übt ein entsprechend hohen Druck aus und schafft es, das Wasser auf ähnlich hohe Position zu drücken.
Das Hydrostatische Paradoxon:
Wie wir gerade gelernt haben, hängt der Schweredruck, der auf einen Körper einwirkt, nur von der Dichte des Mediums und der Eintauchtiefe des Körpers ab.
Diese Erkenntnis führt zu einem anfangs unlogisch erscheinendem Phänomen, das früher als das hydrostatisches Paradoxon bekannt war.
Das folgende Bild demonstriert dieses Phänomen:
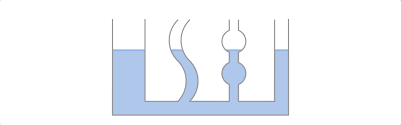
Wir sehen in dem Bild verschieden geformte Gefäße.
Jedes Gefäß ist zur selben Füllhöhe gefüllt mit Wasser.
Wir haben gerade gelernt, dass nun am Boden eines jeden Gefäßes der selbe Druck herrscht.
Das klingt auf den ersten Blick merkwürdig.
Ihr müsst jedoch nun bedenken, dass das Gefäß den Druck des Wasser in schräge Richtungen abfängt.
Alle Kraftkomponenten zur Seite werden abgefangen und nur die Kraftkomponente nach unten bleibt übrig.
Wenn wir die drei Gefäße nun über ein gemeinsames Becken verbinden würden, würde sich bei allen Röhren die selbe Füllhöhe einstellen.
Dieses Phänomen wird “kommunizierende Röhren” genannt.
Es gibt tatsächlich eine Ausnahme Fall beim Hydrostatische Paradoxon:
Das Paradoxon setzt voraus, dass keine Kapillareffekt existieren, also das die Rohre breit genug sind.
Bei sehr kleinen Röhren, z.B. Adern, muss man diese Kapillareffekte tatsächlich mit einkalkulieren.
Darüber wirst du im Studium in der Biophysik noch mal stolpern 🙂
Überprüfe dein Wissen mit diesem Quiz:
Auftrieb:
Mit Hilfe der Schweredruck Formel können wir auch das Phänomen Auftrieb verstehen
Unter Auftrieb versteht man das Phänomen, dass einige Objekte von sich aus schwimmen und andere nicht.
Bevor wir uns die Formel herleiten, stellt euch bitte einen Menschen in einem Schwimmbecken vor.
Dieser würde normalerweise zum Grund des Beckens sinken.
Damit er nicht einsinkt, kann der Mensch versuchen zu schwimmen. Dabei stößt er sich mit seinen Muskeln von der sich umliegenden Wassermasse ab.
Er kann jedoch auch einfach sehr tief einatmen, dann treibt er auf der Wasseroberfläche umher.
Wir haben also im Grunde zwei Möglichkeiten nicht zu ertrinken:
1. Uns abzustoßen durch Muskelkontraktion, oder 2. unsere Dichte zu erniedrigen, indem wir Luft in unseren Körper einlassen um den Auftrieb zu nutzen.
Beide Methoden führen zum selben Ergebnis: Es wirkt eine Netto-Kraft Richtung Oberfläche.
Dies ist auch genau das was der Auftrieb ist, eine Netto-Kraft in Richtung der Wasseroberfläche.
Doch woher kommt diese Netto-Kraft her?
Ihr könnt es euch eigentlich schon denken: Durch die Gravitation!
Die Ursache für den Auftrieb ist der Schweredruck.
Dazu schauen wir uns folgendes Bild an von einem Kubus der vollständig ins Wasser getaucht wurde:
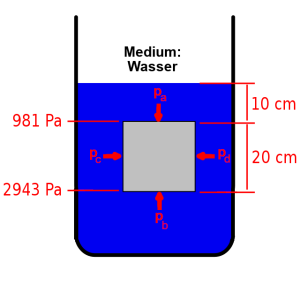
Der Kubus ist h groß, entsprechend ist die Fläche des Würfels A auf allen Seiten gleich groß.
Von allen Seiten drückt das Wasser mit einem anderen Druck \(p_{i}\) gegen den Kubus.
Die gegenüberliegenden Drücke werden aufaddiert.
Nehmen wir mal an, dass der Kubus mit Luft gefüllt ist.
Der Kubus würde nicht zur Seite treiben. Das bedeutet aber, dass der Druck von links und rechts gleich groß sein muss.
Da der Kubus nun leichter ist, als seine Umgebung, würde er an die Oberfläche treiben. Dementsprechend ist der Druck über dem Kubus kleiner als unter dem Kubus.
Dieser Druckunterschied wird alleine durch den Höhenunterschied h verursacht.
Die Auftriebskraft \(F_{A}\) ist die Differenz der Kraft vom Druck unterhalb \(F_{unten}\) und oberhalb des Kubus \(F_{oben}\).
$$ F_{A} = F_{unten} – F_{oben}$$
Woher kriegen wir nun die auf den Körper wirkende Kraft?
Wir kennen doch nur den Schweredruck!
Jedoch ist Druck nichts weiter als wirkende Kraft mal die Fläche, auf die der Druck wirkt.
Es gilt also \(F_{i}=p_{i} \cdot A \).
Wenn wir dies einsetzen können wir A auch gleich ausklammern, weil die Fläche des Würfel oben und unten gleich groß ist.
$$ F_{A} = p_{unten} \cdot A – p_{oben} \cdot A = A \cdot (p_{oben} – p_{unten}) $$
Der Druck p in dieser Gleichung ist der selbe Schweredruck von dem wir vorhin die Formel hergeleitet haben: \(p_{i} = \rho_{Medium} \cdot g \cdot h\),
\(\rho_{Medium}\) ist die Dichte des Mediums in dem sich der Kubus befindet. In unserem Fall wäre das die Dichte von Wasser.
Setzen wir all dies einmal ein und klammern die Dichte des Mediums aus. Durch die Schweredruck-Formel führen wir nun die Wasserhöhe von dem Wasser oberhalb und unterhalb des Kubus ein.
Diese Differenz ist jedoch nichts anderes als die höhe h unseres Kubus:
$$ F_{A} = A \cdot \rho_{Medium} \cdot g \cdot (h_{unten} – h_{oben}) = A \cdot \rho_{Medium} \cdot g \cdot h$$
Das Volumen V eines Körpers ist die Fläche des Körpers A multipliziert mit seiner Höhe h: \(V=A\cdot h\).
Mit der Dichte Definition können wir nun auch ausnutzen, dass die Dichte des Mediums mal das Volumen des Körpers genau das Gewicht des Verdrängten Mediums ausmacht: \(m_{verdrängtes Medium} = V \cdot \rho_{Medium}\).
Masse mal Gravitationsbeschleunigung ist nun einfach Gravitationskraft \(F_{G} = m \cdot g\).
In unserem Fall jedoch ist es nicht die Gewichtskraft des Körpers, sondern die des verdrängten Mediums, für den wir die Gravitationskraft berechnen.
$$ F_{A} = V \cdot \rho_{Medium} \cdot g = m_{verdrängtes \; Medium} \cdot g = F_{verdrängtes \; Medium, G}$$.
Dies ist das sogenannte Archimedische Prinzip.
Die Auftriebskraft eines Körpers entspricht der Gravitationskraft des Mediums das der Körper verdrängt hat!
Das erklärt z.B. warum Schiffe besonders groß sein sollten, um schwimmen zu können oder warum auch der Mensch beim Einatmen anfängt zu nach oben zu treiben.
Sinken, Schweben oder Schwimmen:
Wir haben durch das Archimedische Prinzip nun eine Formel, mit der wir genau klären können, wann ein Körper in einem Medium sinkt, steigt oder gar schwebt.
Alles ist nur eine Frage, wie groß die Gewichtskraft des Körpers gegenüber seiner Aufziehkraft ist.
Das folgende Bild verdeutlicht das Prinzip:
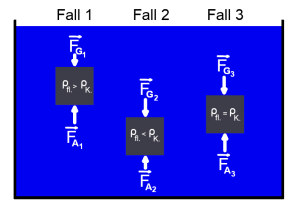
Sinken: \(F_A < F_{Körper,G} \)
Ein Körper sinkt, wenn seine Auftriebskraft \(F_A\) kleiner ist, als der Betrag seiner Gewichtskraft \(F_{Körper,G}\).
Schweben: \(F_A = F_{Körper,G}\)
Ein Körper schwebt, wenn seine Auftriebskraft \(F_A\) gleich groß ist, wie der Betrag seiner Gewichtskraft \(F_{Körper,G}\).
Steigen: \(F_A > F_{Körper,G}\)
Ein Körper steigt dann auf, wenn seine Auftriebskraft \(F_A\) größer ist als seine Gewichtskraft \(F_{Körper,G}\).
Schwimmen ist ein Spezialfall.
Hierbei gelten die selben Bedingungen wie beim Steigen. Jedoch ist das Medium, in dem der Körper aufsteigt, begrenzt.
An der Wasseroberfläche verändert sich dramatisch der Druck von oben, so das der Körper an der Oberfläche schwebt.
Genau diesen Zustand erreichen die Menschen mit ihrer Lunge, beim tiefen Einatmen!
Überprüfe dein Wissen mit diesem Quiz:
Wir würden uns sehr freuen, wenn Du uns ein Feedback zu diesem Abschnitt gibst 🙂
Klicke einfach auf “Start Test” und nimm an der kurzen Umfrage teil.
Vielen Dank!!!
